해시 테이블
해시 테이블과 힙에 대해서 정리해보는 시간을 가지겠습니다
해시테이블의 구조
키(Key)에 데이터(Value)를 매핑할 수 있는 데이터 구조
- 해쉬 함수를 통해, 배열에 키에 대한 데이터를 저장할 수 있는 주소(인덱스 번호)를 계산
- Key를 통해 바로 데이터가 저장되어 있는 주소를 알 수 있으므로, 저장 및 탐색 속도가
획기적으로 빨라짐
- 미리 해쉬 함수가 생성할 수 있는 주소(인덱스 번호)에 대한 공간을 배열로 할당한 후,
키에 따른 데이터 저장 및 탐색 지원
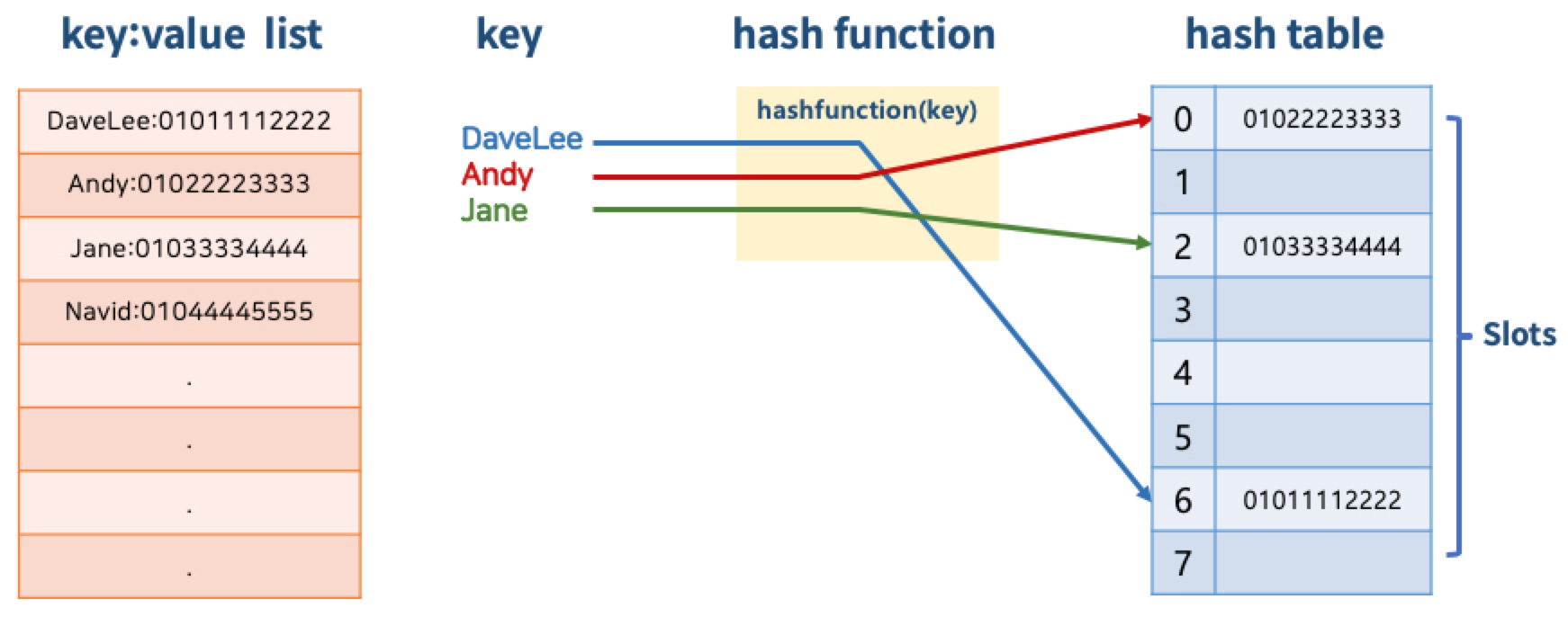
Direct-address table
키의 전체 개수와 동일한 크기의 버킷을 가진 해시테이블을 Direct-address table이라고 합니
다. Direct-address table의 장점은 키 개수와 해시테이블 크기가 동일하기 때문에 해시충돌
문제가 발생하지 않는다는 겁니다. 하지만 전체 키 중 실제 사용되는 키의 개수가 적을 경우
메모리 효율성이 크게 떨어집니다. 대표적인것이 배열 인덱스를 키로 사용하는 방법입니다
충돌
해시함수는 해쉬값의 개수보다 대개 많은 키값을 해쉬값으로 변환하기 때문에 해시함수가 서
로 다른 두 개의 키에 대해 동일한 해시값을 내는 해시충돌(collision)이 발생하게 됩니다. 아
래 그림은 이름-전화번호를 매핑하기 위한 해시함수를 개념적으로 나타냈습니다. 예시의 해시
함수는 ‘daniel’과 ‘bill’를 모두 ‘05’로 매핑해 해시충돌을 일으키고 있습니다.
충돌을 해결하기위해 Separate Chaining
- 키의 해시값 계산
- 해시 값을 이용해 배열의 인덱스를 구한다.
- 같은 인덱스가 있다면 연결 리스트로 연결한다.
나의 한줄평
해시 테이블은 데이터 저장 및 엑세스 효율성이 높아서
코딩테스트에 매우 유용한 데이터 구조이다.
해시테이블 관련문제
- 보석과 돌 https://leetcode.com/problems/jewels-and-stones
- 중복 문자가 없는 가장 긴 부분 문자열 https://leetcode.com/problems/longest-substring-without-repeating-characters
- 상위 K 빈도 요소 https://leetcode.com/problems/top-k-frequent-elements
- 수 찾기 : https://www.acmicpc.net/problem/1920
- 비밀번호 찾기 : https://www.acmicpc.net/problem/17219
힙
힙이란?
- 힙: 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된
완전 이진 트리(Complete Binary Tree)
- 완전 이진 트리: 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리힙의 구조
힙은 최대값을 구하기 위한 구조 (최대 힙, Max Heap) 와, 최소값을 구하기 위한 구조
(최소 힙, Min Heap) 로 분류할 수 있음
- 힙은 다음과 같이 두 가지 조건을 가지고 있는 자료구조임
1. 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다. (최대 힙의 경우)
- 최소 힙의 경우는 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 작음
2. 완전 이진 트리 형태를 가짐힙 과 이진 탐색 트리의 공통점과 차이점
공통점: 힙과 이진 탐색 드리는 모두 이진 트리로 구성되어있다.
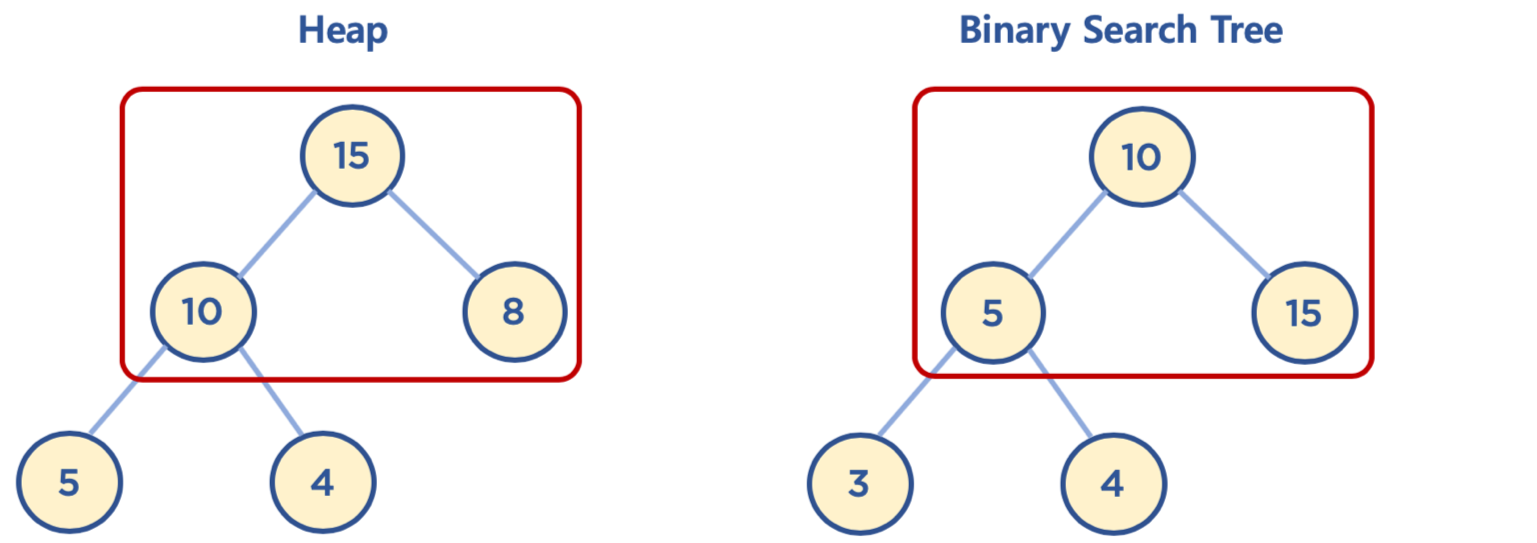
힙에서 데이터 삽입시 기본동작 이해하기
힙 (Heap) 동작
- 데이터를 힙 구조에 삽입, 삭제하는 과정을 그림을 통해 선명하게 이해하기
힙에 데이터 삽입하기 - 기본 동작
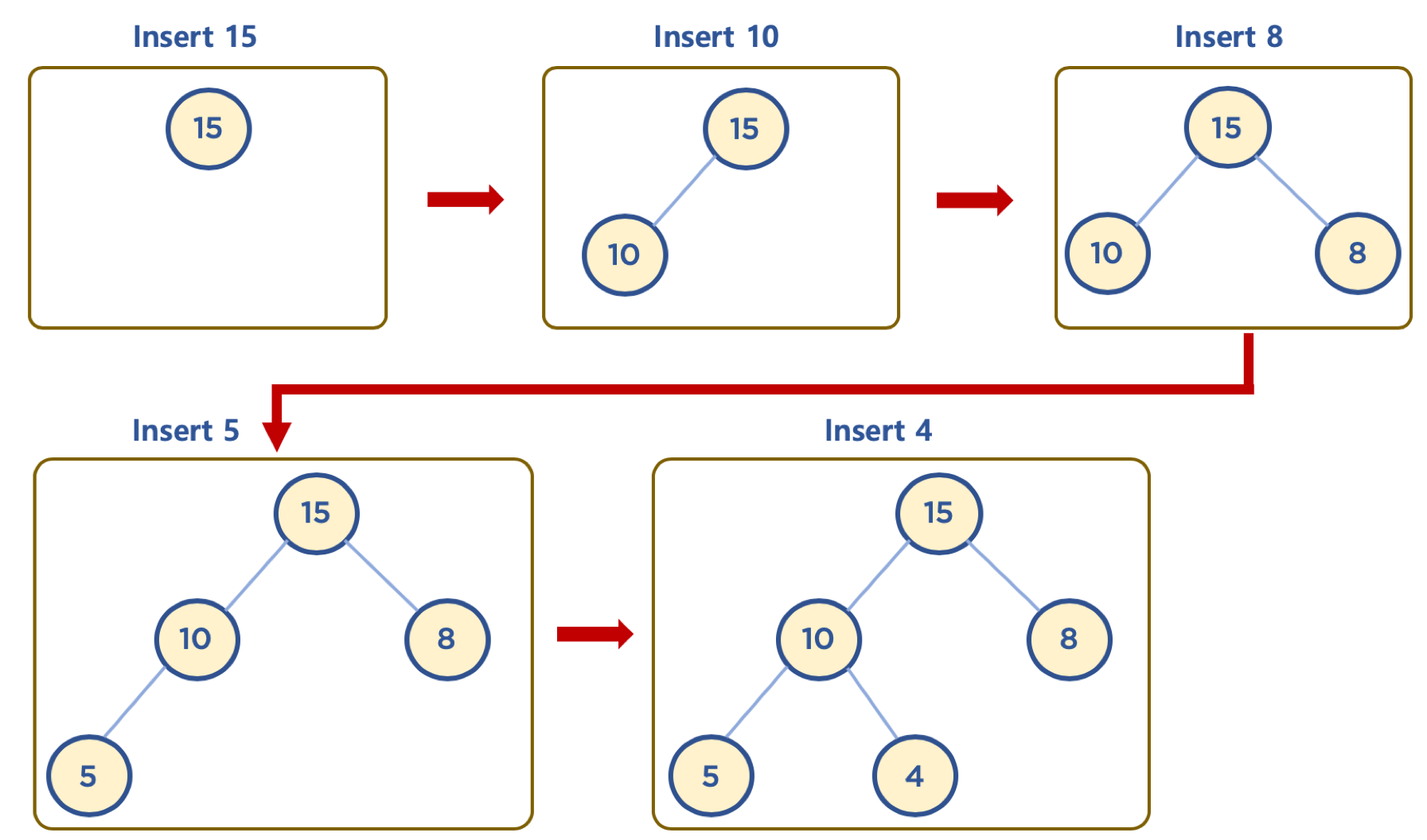
힙에 데이터 삽입하기 -삽입하고자하는 데이터가 더 클 경우 swap
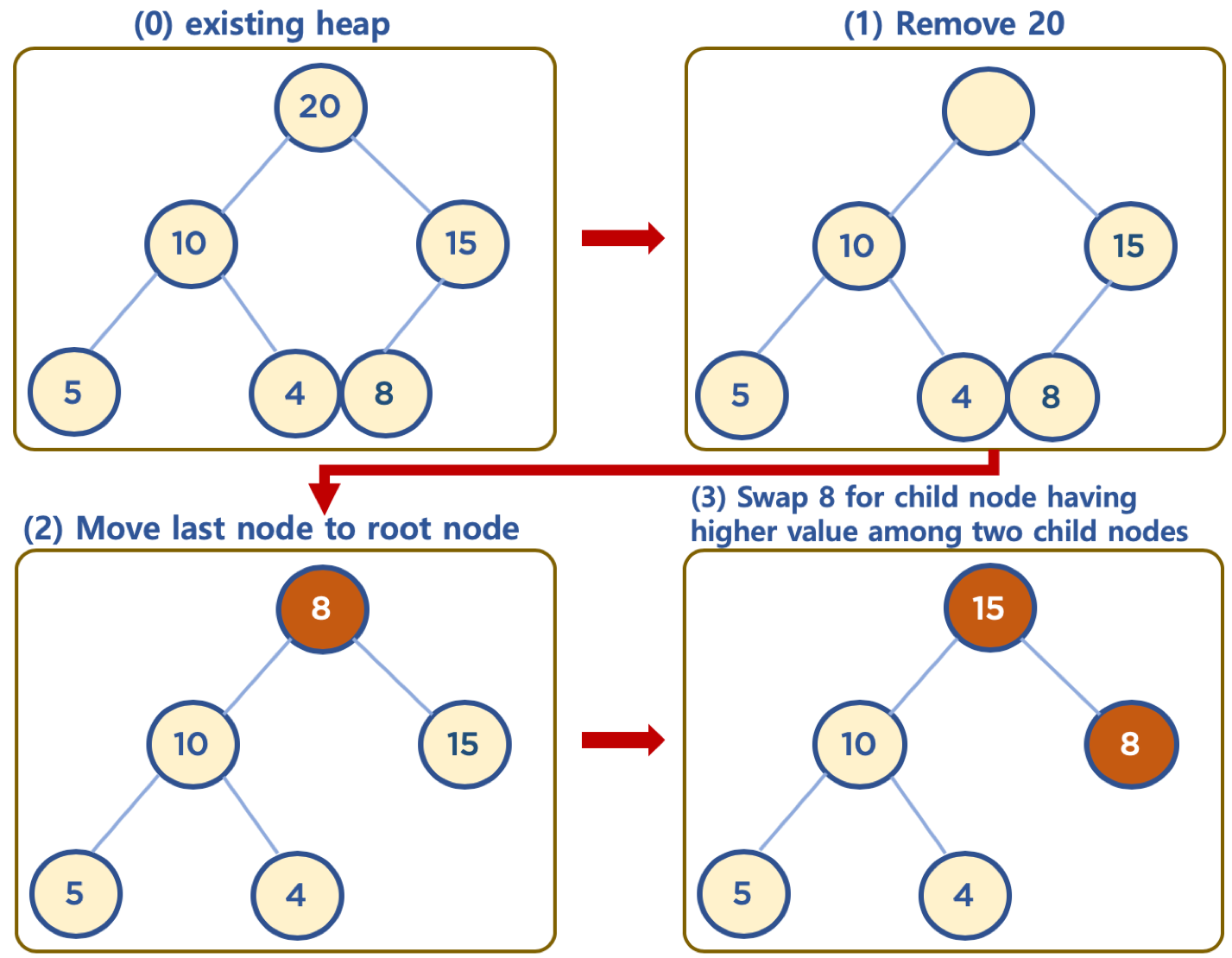
기본 힙 작업을 해보겠습니다.
import heapq
heap =[] # 힙을 초기화해준다.
heapq.heapify(heap) # 빈 목록이 이미 힙이므로 이 단계는 여기서 실제로 중복됩니다.
heapq.heappush(heap,10)
print(heap) [10]
heapq.heappush(heap, 1)
print(heap) [1, 10]
heapq.heappush(heap, 5)
print(heap) [1, 10, 5]
# 가장 작은 요소를 뺴보자
small_heap= heapq.heappop(heap)
print(small_heap) 1
#그럼 이제 5, 10 이남게 된다.
print(heap) [5, 10]배열에서 K번째로 큰 요소
https://leetcode.com/problems/kth-largest-element-in-an-array/description/
- 힙 문제 코드
- 이문제는 대표적인 힙 문제입니다.
#배열에서 K번째로 큰 요소 215번 리트코드
import heapq
from typing import List
#참고로 파이썬은 최소힙만 제공
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
# 이문제는 최소 힙 만들고
# len(heap) -k 해서 나온 값만큼 힙을 pop 하고 남은 heap[0]이 정답
heap =[] # 힙을 초기화해준다.
for num in nums:
heapq.heappush(heap, num)
n = len(heap)-k
for i in range(n):
heapq.heappop(heap)
return heapq.heappop(heap)
# return heap[0] 도 같다 왜나하면 heap[0] 은 항상 제일 작은값
if __name__ == "__main__":
nums = [3,2,1,5,6,4]
k = 2
sol = Solution()
result = sol.findKthLargest(nums, k)
print("Output:", result)'코딩테스트 > 자료구조' 카테고리의 다른 글
| B2805 나무자르기- 이진검색 (0) | 2024.01.19 |
|---|---|
| 그리디 알고리즘을 알아보자 . java.python -> 센서, 동전,강의실,파일합치기 (0) | 2024.01.18 |
| 큐와 스택 (0) | 2024.01.06 |
해시 테이블
해시 테이블과 힙에 대해서 정리해보는 시간을 가지겠습니다
해시테이블의 구조
키(Key)에 데이터(Value)를 매핑할 수 있는 데이터 구조
- 해쉬 함수를 통해, 배열에 키에 대한 데이터를 저장할 수 있는 주소(인덱스 번호)를 계산
- Key를 통해 바로 데이터가 저장되어 있는 주소를 알 수 있으므로, 저장 및 탐색 속도가
획기적으로 빨라짐
- 미리 해쉬 함수가 생성할 수 있는 주소(인덱스 번호)에 대한 공간을 배열로 할당한 후,
키에 따른 데이터 저장 및 탐색 지원

Direct-address table
키의 전체 개수와 동일한 크기의 버킷을 가진 해시테이블을 Direct-address table이라고 합니
다. Direct-address table의 장점은 키 개수와 해시테이블 크기가 동일하기 때문에 해시충돌
문제가 발생하지 않는다는 겁니다. 하지만 전체 키 중 실제 사용되는 키의 개수가 적을 경우
메모리 효율성이 크게 떨어집니다. 대표적인것이 배열 인덱스를 키로 사용하는 방법입니다
충돌
해시함수는 해쉬값의 개수보다 대개 많은 키값을 해쉬값으로 변환하기 때문에 해시함수가 서
로 다른 두 개의 키에 대해 동일한 해시값을 내는 해시충돌(collision)이 발생하게 됩니다. 아
래 그림은 이름-전화번호를 매핑하기 위한 해시함수를 개념적으로 나타냈습니다. 예시의 해시
함수는 ‘daniel’과 ‘bill’를 모두 ‘05’로 매핑해 해시충돌을 일으키고 있습니다.
충돌을 해결하기위해 Separate Chaining
- 키의 해시값 계산
- 해시 값을 이용해 배열의 인덱스를 구한다.
- 같은 인덱스가 있다면 연결 리스트로 연결한다.
나의 한줄평
해시 테이블은 데이터 저장 및 엑세스 효율성이 높아서
코딩테스트에 매우 유용한 데이터 구조이다.
해시테이블 관련문제
- 보석과 돌 https://leetcode.com/problems/jewels-and-stones
- 중복 문자가 없는 가장 긴 부분 문자열 https://leetcode.com/problems/longest-substring-without-repeating-characters
- 상위 K 빈도 요소 https://leetcode.com/problems/top-k-frequent-elements
- 수 찾기 : https://www.acmicpc.net/problem/1920
- 비밀번호 찾기 : https://www.acmicpc.net/problem/17219
힙
힙이란?
- 힙: 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된
완전 이진 트리(Complete Binary Tree)
- 완전 이진 트리: 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리힙의 구조
힙은 최대값을 구하기 위한 구조 (최대 힙, Max Heap) 와, 최소값을 구하기 위한 구조
(최소 힙, Min Heap) 로 분류할 수 있음
- 힙은 다음과 같이 두 가지 조건을 가지고 있는 자료구조임
1. 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다. (최대 힙의 경우)
- 최소 힙의 경우는 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 작음
2. 완전 이진 트리 형태를 가짐힙 과 이진 탐색 트리의 공통점과 차이점
공통점: 힙과 이진 탐색 드리는 모두 이진 트리로 구성되어있다.

힙에서 데이터 삽입시 기본동작 이해하기
힙 (Heap) 동작
- 데이터를 힙 구조에 삽입, 삭제하는 과정을 그림을 통해 선명하게 이해하기
힙에 데이터 삽입하기 - 기본 동작

힙에 데이터 삽입하기 -삽입하고자하는 데이터가 더 클 경우 swap

기본 힙 작업을 해보겠습니다.
import heapq
heap =[] # 힙을 초기화해준다.
heapq.heapify(heap) # 빈 목록이 이미 힙이므로 이 단계는 여기서 실제로 중복됩니다.
heapq.heappush(heap,10)
print(heap) [10]
heapq.heappush(heap, 1)
print(heap) [1, 10]
heapq.heappush(heap, 5)
print(heap) [1, 10, 5]
# 가장 작은 요소를 뺴보자
small_heap= heapq.heappop(heap)
print(small_heap) 1
#그럼 이제 5, 10 이남게 된다.
print(heap) [5, 10]배열에서 K번째로 큰 요소
https://leetcode.com/problems/kth-largest-element-in-an-array/description/
- 힙 문제 코드
- 이문제는 대표적인 힙 문제입니다.
#배열에서 K번째로 큰 요소 215번 리트코드
import heapq
from typing import List
#참고로 파이썬은 최소힙만 제공
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
# 이문제는 최소 힙 만들고
# len(heap) -k 해서 나온 값만큼 힙을 pop 하고 남은 heap[0]이 정답
heap =[] # 힙을 초기화해준다.
for num in nums:
heapq.heappush(heap, num)
n = len(heap)-k
for i in range(n):
heapq.heappop(heap)
return heapq.heappop(heap)
# return heap[0] 도 같다 왜나하면 heap[0] 은 항상 제일 작은값
if __name__ == "__main__":
nums = [3,2,1,5,6,4]
k = 2
sol = Solution()
result = sol.findKthLargest(nums, k)
print("Output:", result)'코딩테스트 > 자료구조' 카테고리의 다른 글
| B2805 나무자르기- 이진검색 (0) | 2024.01.19 |
|---|---|
| 그리디 알고리즘을 알아보자 . java.python -> 센서, 동전,강의실,파일합치기 (0) | 2024.01.18 |
| 큐와 스택 (0) | 2024.01.06 |
